はじめに
Stan Advent Calendar 2018 11日目の記事です。また、タイトルを見て察した人もいるかもしれませんが、Stan Advent Calendar 2018の2日目の記事である、北條大樹さんによるIntroduction to bayesplot (mcmc_ series) の続編でもあります。bayesplotパッケージそのものについては、本記事では説明を省略するため、まずは北條さんの記事をご一読ください。以下引用。
Stanには、既にggplot2ライクな事後処理用の関数が標準装備されています。ここら辺に関しては、以下の資料をご覧ください。
Stanの便利な事後処理関数
これとは別にStan公式が出しているbayesplotパッケージというものがあって、これも同じようなことができます。 既に日本語文献として小杉先生のサイトで紹介されていました(こちら)。上記も併せてご覧ください。この記事を書くうえでも参考にしています。
bayesplotパッケージでは、大きく二つの関数系に分かれています
1. mcmc_ シリーズ(収束や事後分布を確認するための関数群)
2. ppc_ シリーズ(事後予測チェックを行うのに便利な関数群)
この記事では、1.のmcmc_ シリーズの説明を行います。 2.については誰かもしくは未来の自分がやってくれることでしょうw
別に、2.を紹介してしまっても、構わんのだろう?
本記事で採用するモデル
僕はRにデフォルトで用意されているmtcarsというデータセットが好きなので、本記事でもこのデータセットを用います。mtcarsには、32種類の車のデータ(例:燃費mpg、車体重量wt、マニュアル車かオートマ車かam)が格納されています。
head(mtcars) mpg cyl disp hp drat wt qsec vs am gear carb Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4 Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4 Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1 Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1 Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2 Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1
ここでは、燃費を車体重量で予測する、単回帰分析をやってみます。Stanコードは以下の通りです(事前分布は省略しています)。あとで事後予測チェックを行うために、generated quantitiesブロックでy_predという変数を宣言し、今回のモデルに従う乱数を格納させています。
data{ int N; vector[N] Y; vector[N] X; } parameters{ real a; real b; real<lower = 0> sigma; } model{ Y ~ normal(a + b*X, sigma); } generated quantities{ vector[N] y_pred; for(n in 1:N){ y_pred[n] = normal_rng(a + b*X[n], sigma); } }
このモデルをregression.stanという名前で保存してコンパイルしたのち、R上でサンプリングを行います。あとでbayesplotパッケージを用いるので、ここでrstanパッケージと一緒にロードしておきます。
library(rstan) library(bayesplot) stanmodel = rstan::stan_model("regression.stan") standata = list(N = nrow(mtcars), Y = mtcars$mpg, X = mtcars$wt) fit = rstan::sampling(object = stanmodel, data = standata, seed = 1234, iter = 2000, warmup = 1000, chain = 4)
診断
北條さんの記事と同様に、bayesplotパッケージの関数を用いて、収束したかどうか確認してみましょう。切片a、傾きb、標準偏差sigmaの3つのパラメータについて、bayesplot::mcmc_combo()で事後分布とトレースプロットを並べて描画します。サンプリング結果を格納したオブジェクトを、as.array()で配列型にしてから与えることをお忘れなく。
bayesplot::mcmc_combo(as.array(fit), pars = c("a", "b", "sigma"))

便利ですね。
事後予測チェック
さて、ここからが、本記事の本命です。北條さんの記事では紹介されていなかった、ppc_ シリーズの関数を紹介していきます。bayesplotパッケージには、事後予測チェックを手軽に行える関数が、たくさん用意されています。
そもそも事後予測チェック(PPC: Posterior Predictive Check)とは、モデルチェックのための手続きです。
もし何かしらの仮説に基づきモデルを立て、そのモデルが現象をとらえられているとしたら、そのモデルから生成された将来のデータは、今回観測されたデータと似ていることが期待できます。
反対に、モデルから生成した将来のデータが、今回の観測データと似ていないとすると、モデルに改良の余地があるかもしれません。
ppc_ シリーズ
bayesplotパッケージでは、事後予測チェックのための関数は、いずれもppc_ から始まる名前が与えられています。その一覧は、available_ppc()という関数で知ることができます。あるいは公式サイトをご覧ください。
bayesplot::available_ppc() bayesplot PPC module: ppc_bars ppc_bars_grouped ppc_boxplot ppc_data ppc_dens ppc_dens_overlay ppc_ecdf_overlay ppc_error_binned ppc_error_hist ppc_error_hist_grouped ppc_error_scatter ppc_error_scatter_avg ppc_error_scatter_avg_vs_x ppc_freqpoly ppc_freqpoly_grouped ppc_hist ppc_intervals ppc_intervals_data ppc_intervals_grouped ppc_loo_intervals ppc_loo_pit ppc_loo_pit_overlay ppc_loo_pit_qq ppc_loo_ribbon ppc_ribbon ppc_ribbon_data ppc_ribbon_grouped ppc_rootogram ppc_scatter ppc_scatter_avg ppc_scatter_avg_grouped ppc_stat ppc_stat_2d ppc_stat_freqpoly_grouped ppc_stat_grouped ppc_violin_grouped
ppc_シリーズの関数はいずれも、yとyrepという引数を持ちます。
yには、サンプリングのためにStanに渡した目的変数を指定します。
y <- mtcars$mpg
一方yrepには、モデルから生成した乱数を与えます。行列形式でデータが並んでいればよいので、matrix型やdata.frame型でOKです。
行数は、事後予測チェックの描画のために用いる、サンプリングのステップ数です。
列数は、目的変数yと同じ長さ(すなわち、観測されたデータの個数)です。
今回はStanの中で、y_predというベクトルにモデルから生成した乱数を格納したので、以下のようにしてy_predだけを抽出します。この時点でR上ではmatrix型になっているので、このままyrepをppc_シリーズの関数に与えることができます。
yrep <- rstan::extract(fit)$y_pred
ただし、今回は、iter = 2000, warmup = 1000, chain = 4という設定でサンプリングを行ったため、モデルから生成した乱数は、y_pred[1]からy_pred[32]までそれぞれ(2000 - 1000) * 4 = 4000個あるのですが、すべてを描画に使うとごちゃごちゃして見にくくなってしまいますし、、処理もかなり重くなってしまいます。
View(yrep)

そのため一部の関数を用いて描画する際には、一度に使用する行数を絞る(つまり一部の乱数だけを用いる)ことが必要になってきます。
ppc_dens_overlay()
事後予測チェックを行うときに、個人的に便利だなと思うのが、この関数です。ggplot2パッケージのgeom_density()で描けるような分布を、yとyrepそれぞれについて描き、重ね合わせます。10ステップだけ絞り込んで描画を行っていることに注目してください。
bayesplot::ppc_dens_overlay(y = y, yrep = yrep[1:10, ])

色の濃い線で描かれたのが実際に観測されたデータ、薄い線で描かれているのがモデルから生成された乱数です。ピタッと重なっているわけではありませんが、悪くはなさそうです。
ppc_ribbon()
今回の回帰分析のように、目的変数Yに影響を与える説明変数Xが存在する(とモデルを組んでいる)とき、事後予測チェックにおいてはこれらの関係も重要になってくるでしょう。説明変数の変動に対する目的変数の変動の関係は、モデルから生成した乱数に対しても同様に認められるかどうかをチェックしてみましょう。
bayesplot::ppc_ribbon()は、X軸の値に対応するY軸の値が複数存在するとき、それらの区間を描画します。ggplot2::geom_ribbon()と似たようなものですね。今回はモデルから生成した乱数の一部ではなく、すべてを用いて描画してみます。
bayesplot::ppc_ribbon(y = mtcars$mpg, yrep = rstan::extract(fit)$y_pred, x = mtcars$wt, prob = 0.5, prob_outer = 0.95 )

引数probには内側の色の濃い帯、引数prob_outerには外側の薄い帯の描画に使う、パーセンタイルを指定します。最も色の濃い折れ線が、実際に観測された目的変数です。
便利ですね...そういや僕、去年のStan Advent Calendar 2017では、ggfanパッケージを用いて、同様の事後予測チェックを行う記事を書いたんですが、もうbayesplotでいいよね...。
ppc_intervals()
今回使用したmtcarsデータセットは、サンプルサイズが32しかないので、上記のように帯を描くだけでなく、1点1点に対して区間を示すことも可能です。引数はそのまま、関数をppc_intervals()に変えてみましょう。
bayesplot::ppc_intervals(y = mtcars$mpg, yrep = rstan::extract(fit)$y_pred, x = mtcars$wt, prob = 0.5, prob_outer = 0.95 )

その他にも、非常に多くの事後予測チェック用の関数が用意されています。詳しくは公式サイトをご覧ください。
グラフのカスタマイズ
bayesplotパッケージの関数の内部ではggplotオブジェクトを作っているので、以下のようにggplot2の関数を用いてレイヤを追加して、グラフを加工することもできます。以下の例では、任意の切片と傾きを持つ直線を追加するggplot2の幾何学的オブジェクトである、geom_abline()を使用しています。切片と傾きには、それぞれ推定したパラメータの事後平均を用いています。
bayesplot::ppc_intervals(y = mtcars$mpg, yrep = rstan::extract(fit)$y_pred, x = mtcars$wt, prob = 0.5, prob_outer = 0.95) + geom_abline(intercept = mean(rstan::extract(fit)$a), slope = mean(rstan::extract(fit)$b), linetype = "dashed")
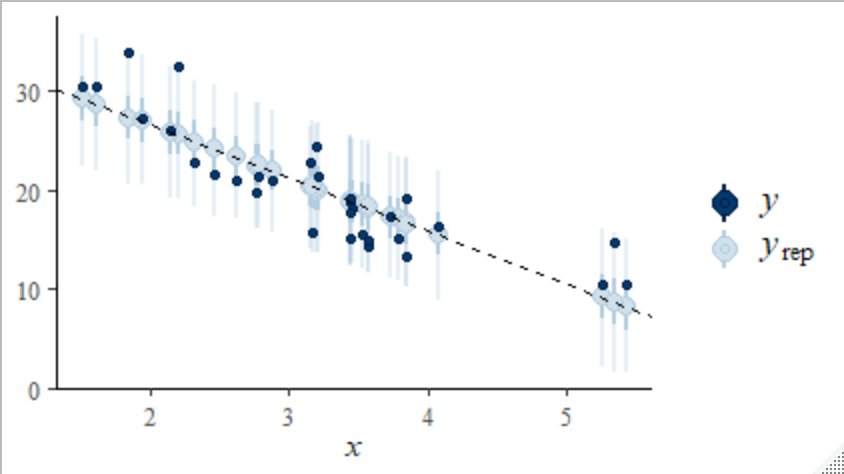
もちろんppc_シリーズの関数だけでなく、mcmc_シリーズの関数でも同様です。以下の例では、themeをbwに変更するとともに、X軸上の任意の位置に垂直線を描くggplot2の幾何学的オブジェクトgeom_vline()を用いて、x = 0の位置に垂直線を描画しています。
bayesplot::mcmc_areas_ridges(as.array(fit), pars = c("a", "b", "sigma"), prob = 0.95, prob_outer = 1) + theme_bw(base_size = 15) + geom_vline(xintercept = 0, linetype = "dashed")

あるいはbayesplotパッケージが用意している、グラフの見栄え(Aesthetics)を調整する関数を用いることも可能です。一覧は公式サイトの「Aesthetics」のところをご覧ください。
例えば直前のグラフは、bayesplotパッケージが用意しているvline_0()という関数を用いて実現することもできます。ついでに、color_scheme_set()という関数で、色調を紫色ベースに変えてみましょう。
bayesplot::color_scheme_set("purple") bayesplot::mcmc_areas_ridges(as.array(fit), pars = c("a", "b", "sigma"), prob = 0.95, prob_outer = 1) + theme_bw(base_size = 15) + vline_0(linetype = "dashed")

現在セットされているカラースキームは、color_scheme_view()でViewerペインに表示させることができます。ちなみにデフォルトのカラースキームは、"blue"です。
bayesplot::color_scheme_view()

また、そのカラーコードはcolor_scheme_get()でコンソールに表示されます。
bayesplot::color_scheme_get() purple 1 #e5cce5 2 #bf7fbf 3 #a64ca6 4 #800080 5 #660066 6 #400040
こんな風に、カスタマイズの余地も残されています。
ただ自分自身では、カラースキームの変更はbayesplot::color_scheme_set()を使いますが、その他のカスタマイズは普通にggplot2の関数を使っています(要はラッパー関数なので)。
他のパッケージとの連携
実はbayesplotパッケージは、brmsパッケージやrstanarmパッケージと非常に相性が良いです(brmsは、プロットにbayesplotパッケージを利用していますし)。これらは、回帰分析や一般化線形モデル、階層線形モデルをRで実行する際の記法と類似した記法で、様々なモデルのパラメータをベイズ推定することを可能にするパッケージです。特にbrmsパッケージはその守備範囲がかなり広く、拡張性も高いため、非常に便利なパッケージです。
これらのパッケージを用いてベイズ推定した際の事後予測チェックについては、Stan Advent Calendar 2018 16日目に投稿予定の、brmsパッケージ入門編の記事で触れる予定です。
おわりに
事後予測チェックは非常に重要な手続きだと思うのですが、それを行うためにggplot2による可視化や、dplyr・tidyrによるデータ整形の技術が必要になってくるとしたら、億劫になって省略してしまうこともあるかもしれません。
bayesplotパッケージは、多くの関数を用意することで可視化の手間を省いてくれる(つまりやってみようと思わせてくれる)、非常に有用なパッケージだと思います。
今回は一部の関数しか紹介できませんでしたが、ぜひ他にも色々と試してみてください。
Enjoy!!