brmsパッケージを用いたベイズモデリング入門
はじめに
本記事は、Stan Advent Calendar 2018 16日目の記事です。brmsパッケージを用いたモデリングの方法や、便利機能、ちょっとしたtipsを紹介します。
brmsパッケージのコンセプトは、
ベイズで(Bayesian)、回帰モデルを(Regression Model)、扱おう、 Stanを使って(using Stan)
です。
読み方はそのまま「ビー・アール・エム・エス」です(僕は勝手にブラムスと呼んでいますが)。
その名の通り、Stanのラッパーパッケージですが、ユーザは自身でStanコードを書く必要はなく、モデルを指定すると自動的に内部でStanコードが生成され、サンプリングが実行されます。
最近は、brmsを用いて分析した論文も見かけるようになってきました。例えば難波修史さんのこの論文とか
- Dynamic Displays Enhance the Ability to Discriminate Genuine and Posed Facial Expressions of Emotion
僕もたまに使っているのですが、あまりにも多機能なので、しっかりと把握できていない部分も多いです。もし本記事に間違いがあればご指摘いただければ幸いです。
brmsパッケージの良いところ
その1
回帰モデルと一言でいっても、実はその守備範囲はかなり広いです。線形モデルも非線形モデルも、その気になればSEMもできるそうです(それならblavaanでいいと思いますが)。
- 一般線形モデル
- 一般化線形モデル
- 階層線形モデル
- その他の自由なモデリング
嬉しいのは、上記の1~3は、多くのRユーザが慣れ親しんでいるであろう記法と同じ記法でモデルを指定できることです。 例えば
- 回帰モデルでは
lm(y ~ x, data = dat) - ポアソン回帰モデルでは
glm(y ~ x, family = "poisson", data = dat) - 階層線形モデルではlme4パッケージやlmerTestパッケ―ジを用いて、
lme4::lmer(y ~ x + (1 | group), data = dat)lme4::glmer(y ~ x + (1 | group), family = "poisson", data = dat)
のように書きますよね。brmsパッケージでも、記法はほぼ同じになります。
その2
デフォルトで用意されている確率分布が、ものっっっっっっっすごく多いです。コンソールで
?brms::brmsfamily
と入力してみてください。用意されている確率分布の一覧が確認できます。 驚くのは、「ベルヌーイ分布とポアソン分布の混合分布である、ゼロ過剰ポアソン分布」等、異なる確率分布を組み合わせた、いわゆる混合分布も多く用意されていることです。通常、このような混合分布を用いたモデリングをStanで書くにはひと手間要るのですが、brmsパッケージでは確率分布を指定するだけで済みます。
また、様々な確率分布からの乱数を生成するための関数や...

確率(密度)を返す関数も用意されています。

その3
「内部で何をやっているのか」を知ることができます。
ベイズを用いる際に最も気になることの一つが、事前分布の設定でしょう。brmsでは、brms::get_prior()で指定したモデルの事前分布を知ることができます。brmsがデフォルトで採用している事前分布も分かるので、報告時に困ることはありません。
また、brms::make_stancode()で指定したモデルのStanコードを出力させることもできます。「この確率分布を使ったモデルをStanで書きたいとき、どうすればいいんだろう」と悩んだとき、brmsで同じ確率分布を使った適当なモデルでStanコードを出力させて、「なるほど、こう書けばいいのか」とヒントを得ることも可能です。
僕が驚いたのが、brms流のガンマ回帰の書き方です。parametersブロックと、modelブロックの一部を以下に抜粋します(事前分布のコードは省略しています)。
parameters { vector[Kc] b; // population-level effects real temp_Intercept; // temporary intercept real<lower=0> shape; // shape parameter } model { vector[N] mu = temp_Intercept + Xc * b; for (n in 1:N) { mu[n] = shape * exp(-(mu[n])); } target += gamma_lpdf(Y | shape, mu); }
modelブロックでは、まず切片と説明変数の線形結合をmuに代入しています。
ガンマ分布にはshapeとrate、2つのパラメータがあり、平均はshape/rateになります。brmsではガンマ回帰におけるデフォルトのリンク関数は対数リンク関数(つまり逆リンク関数は指数関数)なので、exp(mu) = shape/rateの関係があります。
これを変形すると、rate = shape * exp(-mu)になります。
ところがparametersブロックではrateに相当するパラメータはそもそも宣言しておらず、一度別の用途で使ったmuという変数を再利用して上書きしています。あたかも、「もともとのmuには興味ないでしょ」と言わんばかりに。
さらには、そのmuはmodelブロック内で宣言されているため、最終的にrate(に相当する)パラメータを取り出すことができません。なかなか思い切ったことをするなあと思ったのですが、こんな風にbrmsはサンプリング効率を高めるようなStanコードの書き方をしているため、推定がかなり速いです。
その4
他のパッケージとの連携が充実しています。
例えばbrmsはbayesplotパッケージを利用して、brms::pp_check()という関数により、容易に事後予測チェックを行うことができます(詳しくはこちら)。
その他にも、bridgesamplingパッケージを利用してbayes factorを容易に計算できたり、欠測値がある場合にmiceパッケージで多重代入法による補完を行ったあとで、補完したそれぞれのデータセットからサンプリングを行えたりします(詳しくはこちらから)。
brmsパッケージの使用例
それではさっそく、使用例を紹介していきましょう。
インストール & ロード
brmsはCRANに登録されているので、以下でOKです。なお本稿執筆時点における最新バージョンは2.6.0です。
install.packages("brms") library(brms)
上述のbayesplotパッケージやbridgesamplingパッケージ、それからStanをRから扱うためのrstanパッケージを含む、種々の依存パッケージが一緒にインストールされます。便利なものも多いので、初めてStanを使う人は、brmsをCRANからインストールするのが一番楽な気がします (Rtoolsは別途インストールする必要があります)。
2018/12/19追記:
記事を書いた直後にバージョン2.7.0にアップデートされました。"extending support for Gaussian processes"ですって...
一般線形モデル(回帰分析)
まずはベーシックな回帰分析をやってみましょう。サンプルデータは、プリセットのmtcarsです。32台の車の性能が収められたデータセットになります。
head(mtcars) mpg cyl disp hp drat wt qsec vs am gear carb Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4 Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4 Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1 Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1 Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2 Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1
モデルの指定
燃費(mpg)を、車体重量(wt)とマニュアル車かオートマ車か(am)で予測する重回帰分析を試みます。mtcars$amには0か1が格納されていますが、今回はこれらをfactor型に変換したうえで、交互作用項を含むモデルを指定することにします。
mtcars$am <- as.factor(mtcars$am)
stats::lm()を用いると以下のように書きますが...
fit <- lm(mpg ~ wt * am, data = mtcars) summary(fit)
brmsでは、どのようなモデルであっても、統一的にbrm()という関数のなかでモデルを指定します。もちろん、rstan::sampling()でサンプリングする際に指定するような諸々の引数も、brm()は対応しています。例えば、サンプリング回数(iter)、ウォームアップ期間(warmup)、乱数のシード(seed)、チェイン数(chain)など。
fit <- brm(mpg ~ wt * am, data = mtcars, iter = 2000, warmup = 1000, seed = 1234, chain = 4) summary(fit) Family: gaussian Links: mu = identity; sigma = identity Formula: mpg ~ wt * am Data: mtcars (Number of observations: 32) Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1; total post-warmup samples = 4000 Population-Level Effects: Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat Intercept 31.42 3.17 24.90 37.59 2139 1.00 wt -3.79 0.82 -5.37 -2.11 2150 1.00 am1 14.96 4.39 6.66 23.68 1682 1.00 wt:am1 -5.34 1.48 -8.37 -2.50 1828 1.00 Family Specific Parameters: Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat sigma 2.72 0.41 2.09 3.61 1774 1.00 Samples were drawn using sampling(NUTS). For each parameter, Eff.Sample is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence, Rhat = 1).
また、サンプリング結果を格納したオブジェクトをsummary()に入れると要約された結果が返されますが、brms::waic()やbrms::loo()に入れると、WAICやlooを計算することもできます(内部ではlooパッケージを使用して計算しています)。
brms::waic(fit) Computed from 4000 by 32 log-likelihood matrix Estimate SE elpd_waic -78.9 3.9 p_waic 4.1 1.0 waic 157.8 7.9 Warning message: 4 (12.5%) p_waic estimates greater than 0.4. We recommend trying loo instead.
brms::loo(fit) Computed from 4000 by 32 log-likelihood matrix Estimate SE elpd_loo -79.0 4.0 p_loo 4.3 1.1 looic 158.1 7.9 ------ Monte Carlo SE of elpd_loo is 0.1. Pareto k diagnostic values: Count Pct. Min. n_eff (-Inf, 0.5] (good) 31 96.9% 1187 (0.5, 0.7] (ok) 1 3.1% 855 (0.7, 1] (bad) 0 0.0% <NA> (1, Inf) (very bad) 0 0.0% <NA> All Pareto k estimates are ok (k < 0.7). See help('pareto-k-diagnostic') for details.
事前分布の表示
brmsは、いくつかのパラメータについてデフォルトで事前分布を与えていることがあります。今回指定したモデルで、各パラメータにどのような事前分布が与えられていたのかを知るには、brms::get_prior()を使用します。この中にモデルを指定すると、以下のように一覧が表示されます。
brms::get_prior(mpg ~ wt * am, data = mtcars) prior class coef group resp dpar nlpar bound 1 b 2 b am 3 b wt 4 b wt:am 5 student_t(3, 19, 10) Intercept 6 student_t(3, 0, 10) sigma
Interceptの事前分布student_t(3, 19, 10)、19ってどういう根拠で設定されたんでしょうね...。brmsはこんな風に、いくつかのパラメータにデフォルトで弱情報の事前分布を与えていることがあるのですが、どういう根拠に基づいているのかは、まだよく分かっていません。
またbrmsでは基本的に(おそらく常に?)、回帰係数bには事前分布は明示されません。つまりデフォルトでは、無情報事前分布が適用されるということになります。これは後述する「bayes factorの計算」においては問題となるため、そのような場合にはユーザが事前分布を指定する必要がでてきます。
事前分布の指定
ユーザが任意の事前分布を指定したければ、brms::brm()のなかでprior =という引数にパラメータと事前分布をセットで指定します。指定方法には複数の記法があります。詳しくは、コンソール上で?brms::set_priorと入力して、ヘルプをご参照ください。
fit2 <- brm(mpg ~ wt * am, data = mtcars, iter = 2000, warmup = 1000, seed = 1234, chain = 4, prior = c(prior_string("normal(0, 10)", class = "b"), prior(student_t(3, 19, 10), class = Intercept), prior_(~student_t(3, 0, 10), class = ~sigma) ) )
Stanコードの表示
brms::make_stancode()のなかに、事前分布を含み任意のモデルを指定すると、そのStanコードをコンソールに表示してくれます。例えば先ほど事前分布を指定した、以下のモデルのStanコードを表示してみましょう。長いので、ここではmodelブロックだけ掲載します。
ちゃんと、ユーザが指定した事前分布も反映されていますね(target += normal_lpdf(b | 0, 10)という部分)。
brms::make_stancode(mpg ~ wt * am, data = mtcars, prior = c(prior_string("normal(0, 10)", class = "b"), prior(student_t(3, 19, 10), class = Intercept), prior_(~student_t(3, 0, 10), class = ~sigma) ) ) # 以下、出力 -------------------------------------------- model { vector[N] mu = temp_Intercept + Xc * b; // priors including all constants target += normal_lpdf(b | 0, 10); target += student_t_lpdf(temp_Intercept | 3, 19, 10); target += student_t_lpdf(sigma | 3, 0, 10) - 1 * student_t_lccdf(0 | 3, 0, 10); // likelihood including all constants if (!prior_only) { target += normal_lpdf(Y | mu, sigma); } }
そうそう、brmsのStanコードは全て、target +=記法を用いて書かれています。
結果の可視化
plot()
brmsは、サンプリング結果の視覚化にも長けています。rstan::stan_trace()やrstan::stan_dens()のように、描きたいグラフに応じて個別の関数が用意されていることが多いと思いますが、brmsはbayesplotパッケージのbayesplot::mcmc_combo()を用いて結果を可視化します。bayesplotパッケージについては、Stan Advent Calendar 2018の2日目の記事や、11日目の記事をご覧ください。
bayesplot::mcmc_combo()は、各パラメータについて、事後分布とトレースプロットを並べて表示してくれます。
plot(fit)

繰り返しますがこのグラフはbayesplotパッケージを用いて出力されているので、同パッケージの関数を用いて見栄え(Aesthetic)を調整することができます。また、bayesplot::mcmc_combo()と同様に、bayesplotパッケージのmcmc_ シリーズの関数のうち、どの種類の関数を組み合わせて表示するかも選択することができます(mcmc_シリーズについては、Stan Advent Calendar 2018 2日目の記事を参照してください)。ただしmcmc_combo()で表示できるグラフの種類は限られているようです。
例えばこんな風に、色調をピンクに変更し、トレースプロット(bayesplot::mcmc_trace())とチェインごとの事後分布(bayesplot::mcmc_dens_overlay())を並べることもできます。
bayesplot::color_scheme_set("pink") plot(fit, combo = c("trace", "dens_overlay"))

marginal_effects()
※注意:brms 2.11.0より、brms::marginal_effect()がbrms::conditional_effects()に名称変更されています。詳しくはこちら
さらにbrms::marginal_effects()を用いると、「主効果」や「交互作用」を可視化することもできます。今回は交互作用項を含むモデルを指定したので、いわゆる「単純傾斜」も自動的に可視化されます。下のグラフは、左から順に「wtの主効果」「amの主効果」「wtとamの交互作用」を示します。
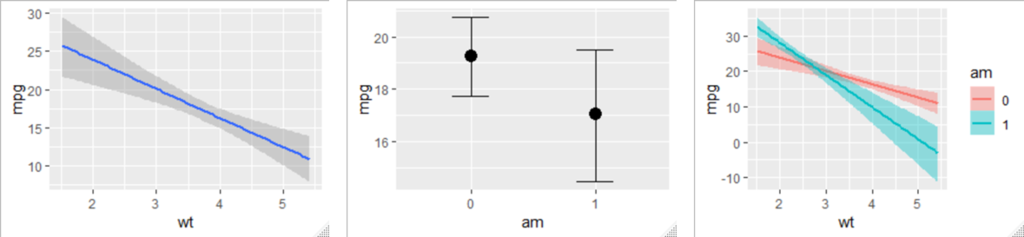
引数effectsに何も指定しなければ、すべての項について可視化が行われますが、特定の項だけを指定することも可能です。また、交互作用項を指定する場合には、その順番を変えることで、どちらの変数についての単純効果を可視化するかも決めることができます。
marginal_effects(fit, effects = "wt:am") #左のグラフ marginal_effects(fit, effects = "am:wt") #右のグラフ

離散変数の場合は(今回はam)、各水準における他方の変数の単純効果が可視化されます。連続変数の場合は(今回はwt)、平均±1SDのポイントにおける、他方の変数の単純効果が示されます。
mean(mtcars$wt) + sd(mtcars$wt) #平均+1SD [1] 4.195707 mean(mtcars$wt) #平均 [1] 3.21725 mean(mtcars$wt) - sd(mtcars$wt) #平均-1SD [1] 2.238793
事後予測チェック
事後予測チェックについては、Stan Advent Calendar 2018 11日目の記事も参照してください。Stanでモデルを書いた場合、事後予測チェックを行うためには、generated quantitiesブロックでモデルから乱数を生成させる手続きが必要になります。その乱数を抽出して、実際に観測されたデータとの類似性を把握するわけですが、なんとbrmsでは、サンプリング結果が格納されたオブジェクトをbrms::pp_check()に入れるだけで、事後予測チェックができます!
brms::pp_check(fit)

Stan Advent Calendar 2018 11日目の記事を読んだ方はお察しの通り、これは内部でbayesplot::ppc_dens_overlay()を使用しています。
他の事後予測チェックにも対応していますよ。type =という引数に、描画形式を指定してみます。
brms::pp_check(fit, type = "error_hist")

これはbayesplot::ppc_error_hist()を使用していますね。
一般化線形モデル
次は、正規分布以外の指数分布族を扱えるように拡張した、一般化線形モデルを例に挙げます。今度は目的変数を、オートマ車かマニュアル車かamにし、説明変数に燃費mpgと重量wtを投入してみます。
stats::glm()と同様に、目的変数が従う確率分布を、引数family =に指定しましょう。今回は、オートマ車かマニュアル車かamは2値の変数なので、family = "bernoulli"とベルヌーイ分布を指定するのがよいように思われます(余談ですが、stats::glm()では2値の目的変数に対しては二項分布(family = "binomial")を指定しますが、brmsでは2値の目的変数に対して二項分布を指定すると、Only 2 levels detected so that family 'bernoulli' might be a more efficient choice.とサジェストされます)。
ただしbrmsでは、family = "binomial"を指定した際の記法がstats::glm()と異なるので、ここでは紹介のためあえて二項分布を適用した書き方をしてみます。
stats::glm()ではこのように書きます。
#amをfactor型に変換していたのを、いったんリセット data(mtcars) fit <- glm(cbind(am, 1 - am) ~ mpg + wt, family = "binomial", data = mtcars) #目的変数が2値の場合は、 #fit <- glm(am ~ mpg + wt, family = "binomial", data = mtcars) でOK summary(fit)
cbind()のなかで何をしているのかというと、総試行数中に占める、成功試行数(am)と失敗試行数(1 - am)の列を指定しています。今回は1台の車がオートマ車かマニュアル車かを予測するので、試行数は1であるため、失敗試行の列は1 - amとしています。
さて、brmsでは、目的変数が二項分布に従うと仮定するとき、以下のように書きます。|の左側には成功試行数を、右側にはtrials()の中に試行数を入れます。
#amをfactor型に変換していたのを、いったんリセット data(mtcars) fit <- brm(am | trials(1) ~ mpg + wt, family = "binomial", data = mtcars) #目的変数が2値の場合は、 #fit <- brm(am ~ mpg + wt, family = "bernoulli", data = mtcars) でOK summary(fit)
brms::marginal_effects()で主効果を可視化してみると、ロジットリンク関数によって、直線ではなく曲線になっていることがわかりますね。

豊富なbrms family
ゼロ過剰ポアソン分布
さて、ここからがbrmsの真骨頂です。stats::glm()ではfamilyに指定できる確率分布は以下の通りです。
- gaussian
- binomial
- Gamma
- inverse.gaussian
- poisson
- quasi
が、brmsでは豊富なfamilyが用意されているということを、冒頭で述べました。試しにちょっと珍しい分布を使ってみましょう。
Mr.Unadon氏がTwitter上で「あなたは、片方しかない靴下を何足もっていますか?」とアンケートをとった結果を拝借します。ネタ元はこちらの片方しかない靴下の数をゼロ過剰ポアソン分布でモデリングしてみたです。
dat <- data.frame(Y = c(rep(0, 746), rep(1, 142), rep(2, 142), rep(3, 154), rep(4, 23), rep(5, 22), rep(6, 9), rep(7, 66) ) ) set.seed(1234) dat$X <- 50 + 2.5*dat$Y + rnorm(n = nrow(dat), mean = 0, sd = 10)
YがUnadon氏が集めた、片方しかない靴下の所持数のデータです。今回のサンプルの中では、ほとんどの人は靴下を片方だけなくすということはないようですね。僕が初めてこのアンケートを見た時、「靴下片方だけどうやって失くすねん」と思ったのですが、最近我が家で片方しかない靴下が発見されました。
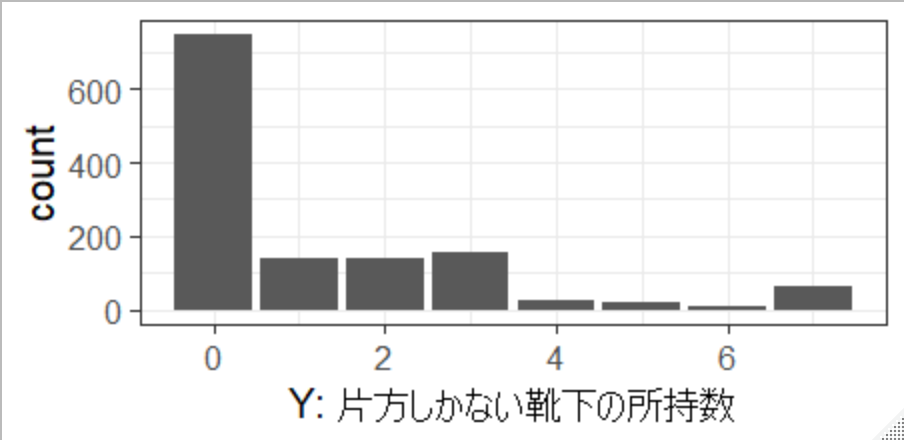
さて、靴下の所持数はカウントデータなので、ポアソン分布と相性がよさそうに思えますが、上図のとおりゼロが圧倒的に多く、通常のポアソン分布の仮定を満たしそうにありません。そこで、ゼロが通常のポアソン分布よりも過剰であるという特徴を捉えた、ゼロ過剰ポアソン分布(zero-inflated poisson)という確率分布を考えます。
ゼロ過剰ポアソン分布は、ベルヌーイ分布とポアソン分布の混合分布です(以下の図はUnadon氏の記事から拝借しました)。靴下を失くすか否かがベルヌーイ分布に従うとと考え、もし失くさないなら当然、片方しかない靴下の所持数の回答は0。もし失くすなら、所持数はポアソン分布に従う、と考えます。なお、ポアソン分布に従う確率変数は0以上の整数をとりうることに注意してください。

一方Xは適当に作った変数ですが、仮に「日常の忙しさ指標(0-100点)」だとしておきましょう。仮定としては、忙しい人ほど靴下を片方なくしやすい、といった具合です。

さて、片方しかない靴下の所持数を、忙しさで予測する、シンプルなモデルを考えてみましょう。ここで、Stanでモデルを書くとしたら、Unadon氏の記事にあるように、target +=という記法を用いて、少し工夫した書き方が必要になります。
しかしbrmsでは、family = "zero_inflated_poisson"を指定するだけです。
fit <- brm(Y ~ X, data = dat, family = "zero_inflated_poisson", seed = 1234) summary(fit) Family: zero_inflated_poisson Links: mu = log; zi = identity Formula: Y ~ X Data: dat (Number of observations: 1304) Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1; total post-warmup samples = 4000 Population-Level Effects: Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat Intercept -1.64 0.16 -1.98 -1.33 2039 1.00 X 0.04 0.00 0.04 0.05 2283 1.00 Family Specific Parameters: Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat zi 0.47 0.02 0.43 0.50 1868 1.00 Samples were drawn using sampling(NUTS). For each parameter, Eff.Sample is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence, Rhat = 1).
事後予測チェックしてみましょう。
brms::pp_check(fit)
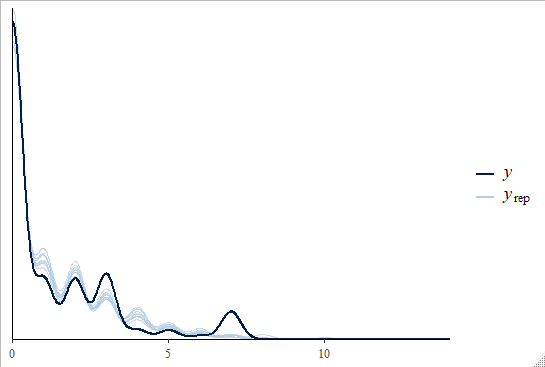
いい感じですね。
階層線形モデル
本記事冒頭でも言及したように、lme4パッケージやlmerTestパッケ―ジを用いると、以下のように書きますよね。
lme4::lmer(y ~ x + (1 | group), data = dat)lme4::glmer(y ~ x + (1 | group), family = "poisson", data = dat)
brmsでは、関数をbrm()に変えるだけなので、本記事では説明を省略します。
モデル比較
brmsパッケージを用いてサンプリングした結果を利用して、モデル比較を行ってみます。モデル比較には様々な観点がありますが、ここではbayes factorを指標とすることにします。bayes factorについては、北條大樹さんのこちらの記事や、清水裕士さんのスライドをご参照ください。
brmsを用いてモデル比較するために、kidneyというデータセットを用いて、試してみましょう。survivalパッケージにも同じ名前のデータセットがあるので、区別するためにbrms::kidneyと指定したほうが無難です。
話を簡単にするために、ここでは目的変数に「病気の再発までの時間time」、説明変数に「患者の年齢age」を投入した、単回帰分析を考えます。また、本当は右側打ち切り(right-censored)が起こっているため、それを考慮したモデリングをするべきですが、打ち切りが起こっていないデータだけを抽出しています。
なおbrmsでは、brm(y | cens(censored) ~ x, data = dat)のように書くことで、打ち切りデータのモデリングも容易に実現できます(cens()のなかに、打ち切りの有無を判別する変数を投入します)。
#データセットの作成 --------------------------------------------- #1回目の再発までの時間 & 非打ち切りデータのみを使用 dat <- brms::kidney %>% dplyr::filter(recur == "1" & censored == 0) #データセットの行列数 ------------------------------------------- dim(dat) #38人分のデータが抽出された [1] 38 7 #冒頭6行分を表示 ------------------------------------------------ head(dat) time censored patient recur age sex disease 1 8 0 1 1 28 male other 2 23 0 2 1 48 female GN 3 22 0 3 1 32 male other 4 447 0 4 1 31 female other 5 30 0 5 1 10 male other 6 24 0 6 1 16 female other
目的変数timeの分布はこのように左に歪んでいます。

正規分布を仮定したモデル
まずはベーシックな単回帰分析を実行してみます。目的変数が正規分布に従うと想定することになるので、family = "normal"と指定します(familyを指定しなければ自動的に正規分布を仮定することになるので、省略も可能です)。
さらに以下3点を対処する必要があります。
- 全パラメータに、無情報でない事前分布を指定
iterを多めに- 正確には、有効なMCMCサンプルの数を多めに(2109/12/6追記)
save_all_pars = TRUEと引数を指定
モデルはこのようになります。
fit_n <- brm(time ~ age, family = "normal", prior = prior(normal(0, 5), class = b), seed = 1234, iter = 100000, warmup = 5000, data = dat, save_all_pars = TRUE)
事後予測チェックを行ってみましょう。
brms::pp_check(fit_n)

実際に観測されたデータとズレがありますね。上のヒストグラムを見ればわかる通り、今回はtimeが正規分布に従うと仮定するのは、適切ではないかもしれません。
最後にbrms::bridge_sampler()を用いて、bridge samplingによる対数周辺尤度を計算してみましょう。これは内部ではbridgesampling::bridge_sampler()を利用しています。
brms::bridge_sampler(fit_n) Iteration: 1 Iteration: 2 Iteration: 3 Iteration: 4 Bridge sampling estimate of the log marginal likelihood: -249.9636 Estimate obtained in 4 iteration(s) via method "normal".
ワイブル分布を仮定したモデル
brms::kidneyは生存時間解析に適したデータセットなので、比較対象として、パラメトリックな生存時間解析でよく用いられる、ワイブル分布を適用したモデルを考えてみます。
fit_w <- brm(time ~ age, family = weibull(), prior = prior(normal(0, 5), class = b), seed = 1234, iter = 100000, warmup = 5000, data = dat, save_all_pars = TRUE)
事後予測チェック。
brms::pp_check(fit_w)

先ほどよりマシになった気がしますね。
次はbridge samplingによる対数周辺尤度の計算。
brms::bridge_sampler(fit_w) Iteration: 1 Iteration: 2 Iteration: 3 Iteration: 4 Bridge sampling estimate of the log marginal likelihood: -232.0824 Estimate obtained in 4 iteration(s) via method "normal".
正規分布 vs ワイブル分布
いよいよモデル比較です。各モデルの対数周辺尤度に、いったん-1を掛けます。つまり、自由エネルギーとして計算します。
「自由エネルギーの差」の指数をとるとbayes factorになります。
fe_n = -1 * brms::bridge_sampler(fit_n)$logml #正規モデルの自由エネルギー fe_w = -1 * brms::bridge_sampler(fit_w)$logml #ワイブルモデルの自由エネルギー exp(fe_n - fe_w) #bayes factor [1] 58278089
今回のデータに対する当てはまりの観点では、正規分布を仮定したモデルに対して、ワイブル分布を仮定したモデルを支持する程度が、58278089倍...もう圧倒的に大きいと考えられます。
ただしbrmsは、bridgesampling::bayes_factor()を利用して直接bayes factorを計算する、brms::bayes_factor()という関数を用意しています。引数x1とx2に、各モデルのサンプリング結果を格納したオブジェクトを指定してください。
brms::bayes_factor(x1 = fit_w, x2 = fit_n) Iteration: 1 Iteration: 2 Iteration: 3 Iteration: 4 Iteration: 1 Iteration: 2 Iteration: 3 Iteration: 4 Estimated Bayes factor in favor of bridge1 over bridge2: 58273598.05176
やはり今回のデータに対する当てはまりの観点では、正規分布を仮定したモデルよりも、ワイブル分布を仮定したモデルのほうが良いと考えられます。
こんな風に、brmsを用いてモデル比較をすることもできます。ただしモデル比較という手続きは非常に難しいので、実際にはもっと慎重に行う必要があると思います。 以下、北條さんの記事から引用します。
ベイズファクターの注意点
- ベイズファクターは事前分布の影響をかなり大きくうけます 。
→ 同一データ、同一モデルで事前分布のみを変化させた場合に、
どれだけベイズファクターが変化するかを検討するととてもよくわかります。
- bridgesamplingパッケージでも計算がうまく行かないことはありますので、
全てのモデル間のベイズファクターが計算できるわけではありません。
- モデル比較を行うのはとても難しいです。
本来、我々が、比較すべきモデルは無限に存在します。
- ベイズファクターは、2つのモデル間の比として考えるので、
それ以外のモデルについては考えてはいません。
2019/12/6追記
清水裕士さんによる、Stan Advent Calendar 2019 6日目の記事:brmsパッケージで安易にベイズファクターを使うと死ぬ話で、brmsでベイズファクターを求める際の注意点が書かれています。
その他のtips
Stanコードの保存
brms::brm()でサンプリングを行う際に、save_model = "hogehoge"と引数を追加してみましょう(もちろんhogehogeのところは任意の名前で構いません)。
fit_w <- brm(time ~ age, data = dat, save_model = "hogehoge")
するとカレントディレクトリに、hogehogeという名前のファイルができていると思います。R上でこのファイルを開くと、brms::make_stancode()で生成できるようなStanコードが記録されていることが分かります。
仮にbrmsのバージョンが変わったとしても、少なくとも今回のサンプリングを実行した時点でのStanコードは判明しているので、結果の再生可能性の向上に寄与するかもしれません。

サンプリング結果の保存
brms::brm()でサンプリングを行う際に、file = "fugafuga"と引数を追加してみましょう(もちろんfugafugaのところは任意の名前で構いません)。
fit_w <- brm(time ~ age, data = dat, file = "fugafuga")
するとカレントディレクトリに、fugafuga.rdsという名前でサンプリング結果が保存されています。
以下のようにreadRDS()という関数で、あとでロードすることができるので、「しまった、うっかりRStudioを閉じてしまった!」なんて心配も不要です。また、例えばサンプリング結果をRMarkdownでまとめたい場合などにも重宝すると思います。
fit_again <- readRDS("fugafuga.rds")
関数名の前に「brms::」と付けるクセをつける
あくまで個人的な意見ですが、何かしらのパッケージ内の関数を使用する場合には、パッケージ名を併記したほうがいいと思っています(例えばdplyr::select()とか)。これはいくつかの理由がありますが、一番の理由は、たまに複数のパッケージ間で同じ名前の関数が存在することがあるからです。例えばfilter()という関数は、少なくともstatsパッケージとdplyrパッケージに存在します。
また、他者とコードを共有するときに、何のパッケージの関数か分からないと混乱を招くと思うので、そういった意味でもパッケージ名を明示しておいた方がいいかなと思っています。
もちろん、文字数が増えるのでコードが見にくくなるという側面もありますが。
ただ、brmsを用いる際には、特に意識してbrms::と書いたほうがよいと思います。これは何故かというと、brmsは様々なパッケージに依存しているのですが、データセット名や関数名が衝突することがあるからです。例えば以下のようなデータセットや関数たち。
brms::kidneyデータセットとsurvival::kidneyデータセットbrms::bayes_factor()とbridgesampling::bayes_factor()brms::bridge_sampler()とbridgesampling::bridge_sampler()brms::bf()とbridgesampling::bf()
一番タチが悪いのが最後のbf()です。bridgesampling::bf()はbayes factorを計算する関数で、bridgesampling::bayes_factor()の略称なのですが、brms::bf()はbayes factorとは関係がありません。brms::bf()は、brms::brmsformula()の略称で、brmsを用いて高度なモデリングを可能にするための関数です。
分位点回帰を例に説明しましょう。brmsは、分位点回帰も容易に実行することができます。その場合、asymmetric Laplace分布を適用して、以下のように書きます。brm()のなかに、さらにbf()という関数を書いて、その中でモデルを指定します。
fit <- brm(bf(y ~ x, quantile = 0.2), data = dat, family = asym_laplace() )
これ、bridgesampling::bf()のほうが読み込まれてしまうと、当然エラーになります。したがって以下のように、brms::bf()であることを明示したほうが無難です。
fit <- brm(brms::bf(y ~ x, quantile = 0.2), data = dat, family = asym_laplace() )
あるいは、パッケージの優先順位をつけてもいいかもしれないですね。
参考記事:R でパッケージの優先順位を変えたい #rstatsj
おわりに
ここで紹介した機能は、brmsのほんの一部にすぎません。モデリングの自由度もかなり高いですし、ユーザも多いのでWeb上で色んな情報を得ることができます。 例えばこちらの記事では、brmsを用いて信号検出理論のパラメータを推定しています。
きっとこれからも、どんどん新しい機能が追加されていくと思うので、要チェックですね。
そういえば、この記事を書くためにbrmsについて調べていたら、brmsとggplot2とtidyverseを用いてStatistical Rethinkingを解説しているドキュメントを見つけました。
Statistical Rethinking with brms, ggplot2, and the tidyverse
ざっと見たところ、brmsの具体的な使用例についても紹介しているようです。参考にしてみてください。
Enjoy!!